Построение призмы в перспективе

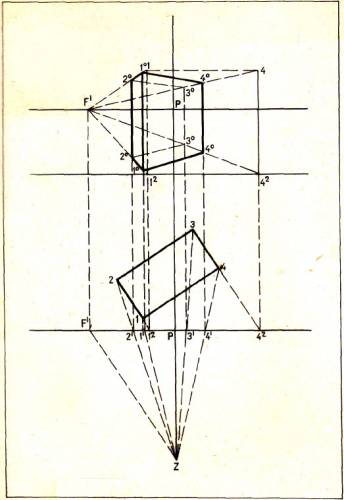
Построение четырехгранной призмы в перспективе в случайном положении по заданным размерам

Если на рисунке надо изобразить в перспективе призму в любом повороте по точно заданным размерам, то можно применить способ, показанный на рисунке.

Построим в плане основание призмы желаемого размера под заданным углом к картинной плоскости. Выберем точку зрения Z. Для определения точки схода одного из направлений горизонтальных ребер призмы проведем через точку Z прямую, параллельную с направлением 1—2 и 3—4 до пересечения с линией горизонта в точке F¹. Так как вторая точка схода находится за пределами картины, то можно применить такой способ, когда ею не пользуются. Для этого продолжим направления ребер призмы 1—2 и 3—4 до линии основания картины, найдя 1² и 4². Перенесем точки 1² и 4² на основание картины, где будет построено перспективное изображение. Точку схода F¹ перенесем на линию горизонта картины. Соединим точки 1² и 4² с точкой схода F¹. От точки 4² отложим вверх высоту призмы так как если бы она стояла на основании картинной плоскости. Получим точку 4, затем таким же путем получим точку 1 и соединим их с F¹ . Высота призмы на любом удалении в глубину картины будет определяться расстоянием между линиями 4 — F¹ и 4²— F¹. Соединив на плане вершины углов призмы 1, 2, 3, 4 с точкой зрения Z, на пересечении с картинной плоскостью мы получим 2¹ — З¹ и 1¹ — 4¹, соответствующие перспективным сокращениям сторон призмы. От точек 1¹, 2¹, 3¹, 4¹ проводим вертикали до пересечения с направлениями 1² —F¹и 4²—F¹. Тем самым получим в перспективе основание четырехугольника 1°, 2°, 3°, 4°. На продолжениях тех же вертикалей при их пересечении с направлениями 4— F¹ и 1—F¹ найдем верхнее основание призмы, чем и будет закончено ее построение. Рекомендуем сделать с натуры зарисовки шкатулки, шкафа и других прямоугольных предметов и проверить правильность их перспективных построений на основании полученных знаний. При проверке следует нанести на рисунок линию горизонта и точки схода.