Деление прямых и линий плоскостей на равные и пропорциональные части в перспективе
Иногда при работе над картиной встречается необходимость разметить равные расстояния на линиях, удаляющихся к точке схода. Нами показано, как можно определить интервалы между столбами, расположенными под любым углом к картинной плоскости.
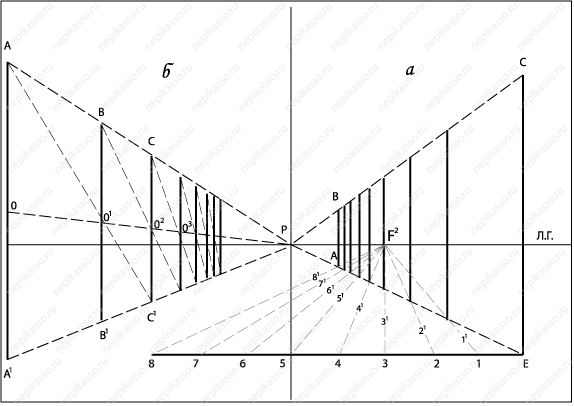
Остается от этих точек провести прямые, параллельные АВ, до пересечения с линией ВС (проходящей через точку Р), и мы найдем расположение остальных столбов.
Используя помещенные здесь способы, рекомендуем нарисовать и проверить перспективную правильность изображения аллеи с деревьями на равных расстояниях, колоннады, столбов ограды. На рисунках, которые были сделаны раньше для уяснения применения правил проведения параллельных удаляющихся линий, мы рекомендуем проверить размещение окон и простенков, а также столбов забора. На рисунке показано деление плоскости АВСЕ на пропорциональные части.
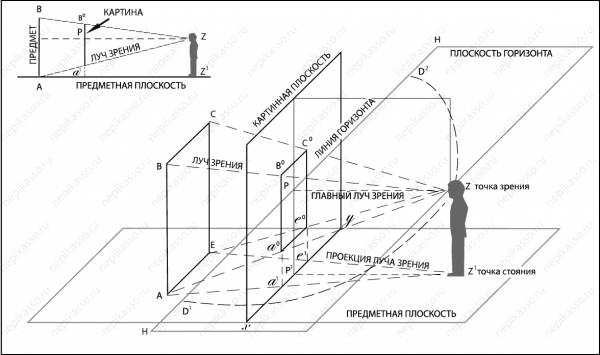
Точки отдаления D1
и D2
Все перспективные изображения
горизонтальных линий, имеющих направление под углом в 45° к плоскости картины,
сходятся в точках отдаления
D1 и D2, которые всегда находятся на линии горизонта.
Расстояния их от главной точки схода Р будут равны
D1
P и D2P, то есть
расстоянию рисующего до картины. При помощи
точек D1 и D2 измеряют величину прямых линий, перпендикулярных к картинной
плоскости.
Построим перспективу квадрата
фронтального положения, пользуясь точкой D1
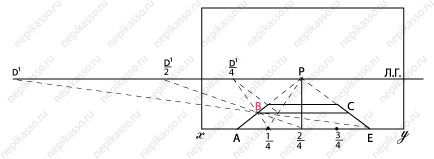
Даны сторона квадрата АЕ на
основании картинной плоскости, линия горизонта, положение точки Р и за
пределами картины точка отдаления D1
.
Требуется построить квадрат АВСЕ
во фронтальном положении. Точки А и Е соединим с точкой Р
и тем самым получим в перспективе направления сторон квадрата АВ и ВС. Точку Е соединим с точкой
D1
и на пересечении с
направлением АР найдем угол квадрата — В. Через точку В
проведем горизонтальную прямую до пересечения с направлением ЕР
в точке С, завершив тем самым построение
квадрата АВСЕ.